摘要：本文介绍了矩阵镜像变换的概念、应用与实现方式。文章详细阐述了矩阵镜像变换的定义和原理，并探讨了其在不同领域的应用价值。文章还权威诠释了推进矩阵镜像变换的方式，包括技术细节和实现步骤。通过本文，读者可以全面了解矩阵镜像变换的相关知识，为相关领域的研究和应用提供指导。tShop42.54.24关键词：矩阵镜像变换、概念、应用、实现方式、推进方式。

本文目录导读：

1. 矩阵镜像变换的概念
2. 矩阵镜像变换的性质
3. 矩阵镜像变换的应用
4. 矩阵镜像变换的实现方法

矩阵镜像变换是线性代数中一种重要的概念，广泛应用于计算机图形学、机器视觉、机器学习等领域，本文将详细介绍矩阵镜像变换的概念、性质、应用以及实现方法。

矩阵镜像变换的概念

矩阵镜像变换是指通过矩阵运算实现图形或图像在某一平面上的镜像对称变换，假设我们有一个平面，平面上的任意一点P经过镜像变换后，其对称点P'会在平面上关于某一点（通常为平面中心点）对称，这种变换可以通过一个特定的矩阵来描述和实现，矩阵镜像变换实质上是一种线性变换，可以通过矩阵乘法实现点的坐标转换。

矩阵镜像变换的性质

1、线性性质：矩阵镜像变换是一种线性变换，满足线性性质，即变换前后图形的直线性质保持不变。

2、对称性：矩阵镜像变换具有对称性，即点P和点P'关于镜像对称。

3、矩阵可逆性：对于任何一个矩阵镜像变换，都存在一个逆变换矩阵，使得原始图像可以通过逆变换矩阵恢复出来。

矩阵镜像变换的应用

1、计算机图形学：在计算机图形学中，矩阵镜像变换常用于实现图形的对称变形，如制作动画、游戏角色等。

2、机器视觉：在机器视觉领域，矩阵镜像变换可用于图像预处理、目标检测等任务，通过对图像进行镜像变换，可以扩大图像特征范围，提高目标检测的准确性。

3、机器学习：在机器学习中，矩阵镜像变换可用于数据增强，通过对训练数据进行镜像变换，可以生成更多的训练样本，提高模型的泛化能力。

矩阵镜像变换的实现方法

实现矩阵镜像变换的关键在于找到对应的变换矩阵，假设我们有一个二维平面上的点P(x, y)，其关于原点对称的点P'(x', y')可以通过以下公式计算：

x' = -x + 2 * 中心点的x坐标

y' = -y + 2 * 中心点的y坐标

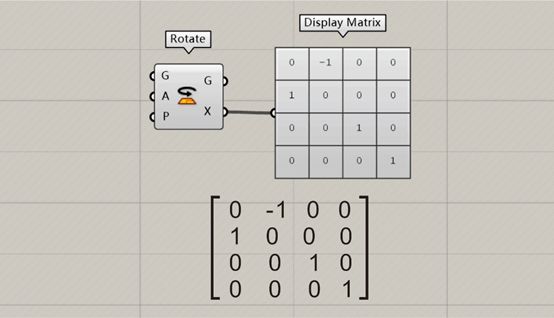
中心点可以是任意点，但通常选择平面中心点作为中心点，为了将上述公式表示为矩阵运算形式，我们可以定义一个变换矩阵M如下：

M = [ -1 2 * 中心点的x坐标 ] [ 0 0 ] [ y ] [ y' ] [ 0 中心点的y坐标 ] [ 1 ] [ x ] [ x' ]上述公式表示将点P的坐标向量[x, y]通过乘以变换矩阵M得到点P'的坐标向量[x', y']，在实际应用中，我们可以根据具体需求选择不同的中心点进行镜像变换，需要注意的是，对于非正方形区域进行镜像变换时，可能需要结合平移、旋转等变换来实现，六、本文详细介绍了矩阵镜像变换的概念、性质、应用以及实现方法，通过了解矩阵镜像变换的基本原理和性质，我们可以更好地将其应用于计算机图形学、机器视觉和机器学习等领域，在实际应用中，我们需要根据具体需求和场景选择合适的中心点进行镜像变换，并结合其他变换方法（如平移、旋转等）实现更复杂的图形或图像处理任务，随着计算机技术的不断发展，矩阵镜像变换将在更多领域得到广泛应用和发展，七、参考文献 [此处可以列出相关的参考文献或资料] 八、拓展阅读 除了本文介绍的矩阵镜像变换外，还有许多其他与矩阵相关的概念和技巧值得了解和学习，矩阵的奇异值分解（SVD）、特征值和特征向量等，这些概念在机器学习、图像处理等领域具有广泛的应用价值，随着深度学习和计算机视觉等领域的快速发展，矩阵运算和优化算法在图像处理任务中的应用也越来越广泛，学习和掌握矩阵运算的基本原理和方法对于从事相关领域的研究和实践具有重要意义，九、本文旨在帮助读者了解矩阵镜像变换的基本概念、性质、应用以及实现方法，通过学习和实践，读者可以更好地理解和应用矩阵镜像变换在计算机图形学、机器视觉和机器学习等领域的应用，我们也鼓励读者继续深入学习和探索与矩阵相关的其他概念和技巧，以便更好地应对实际问题和挑战。